B-TREE即平衡多路查找路(B->balance),一颗m阶的B-TREE有如下的特征：

1) 树中每个结点至多有m个孩子；

2) 除根结点和叶子结点外，其它每个结点至少有有ceil(m / 2)个孩子；

3) 若根结点不是叶子结点，则至少有2个孩子（特殊情况：没有孩子的根结点，即根结点为叶子结点，整棵树只有一个根节点）；

4) 所有叶子结点都出现在同一层，叶子结点不包含任何关键字信息(可以看做是外部结点或查询失败的结点，实际上这些结点不存在，指向这些结点的指针都为null)；

5) 每个非终端结点中包含有n个关键字信息： (n，P0，K1，P1，K2，P2，......，Kn，Pn)。其中：

a) Ki (i=1...n)为关键字，且关键字按顺序排序K(i-1)< Ki。

b) Pi为指向子树根的接点，且指针P(i-1)指向子树种所有结点的关键字均小于Ki，但都大于K(i-1)。

c) 关键字的个数n必须满足： ceil(m / 2)-1 <= n <= m-1。

B-TREE的查询操作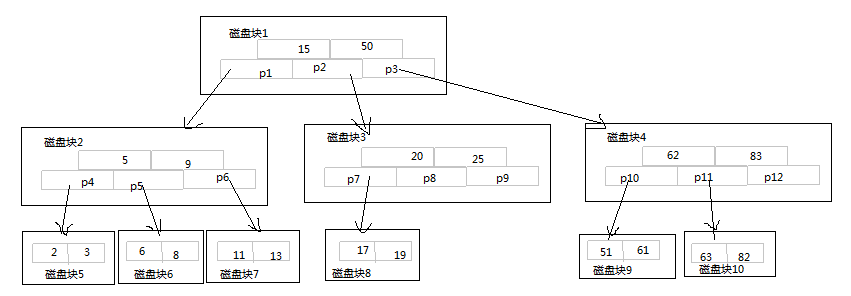

首先把磁盘块1导入到内存中，通过折半查找,找到P3指针(50<51)
通过P3指针找到磁盘块4，将磁盘块4导入内存中，通过折半查找P10指针(51<62)
通过P10指针找到磁盘块9，将磁盘块9导入内存中，通过值班查找找到51
至此，整个查找过程就结束了，这个过程一共进行了三次磁盘IO

B-TREE的添加操作

插入一个元素时，首先在B-TREE中是否存在，如果不存在，先判断叶子节点的空间是否足够，如果足够，就往叶子节点里面添加，如果不够，就需要分裂页操作。
分裂页将一半数量的关键字分裂到新的叶子节点，同时将中间节点更新到父节点中，这时候需要分两种情况，如果父节点还没满，就直接插入，如果父节点已经满，
需要分裂页，父节点中间节点更新到爷爷节点，整个过程以此类推。直到整棵树平衡。

B-TREE的删除操作

A、删除节点在叶子节点上
A.1)如果被删除关键字所在结点的原关键字个数n>=ceil(m/2)，直接删除该节点的关键字。
A.2)如果被删除关键字所在结点的关键字个数n等于ceil(m/2)-1，那么需要看看兄弟节点
    A.2.1.如果兄弟节点关键字>=ceil(m/2),采用覆盖操作，父节点覆盖删除节点，兄弟节点最值覆盖原来的父节点
    A.2.2.如果兄弟节点关键字=ceil（m/2),需要把兄弟节点与父节点合并作为新节点，合并后可能导致父节点不符合B-TREE结构要求，
          需要继续合并，直到B-TREE满足条件。
B、删除的节点不在叶子节点上，可以通过将左子书的最大关键字（右字数的最小节点）K-max覆盖到要删除的节点key-parent。
   接下来问题相当于转成删除key-max节点的问题，步骤转向A

B+TREE是B-TREE的一种优化

一颗m阶的B+TREE和B-TREE异同点：
1、有n棵子树的节点包含n-1个关键字(此处有争议，部分教材是n-1个关键字，但是部分教材是n个关键字)
2、所有关键字以及值都放在叶子节点中(非叶子节点相当于索引)

B+TREE的添加操作分成三种情况

A)如果叶子节还没满，直接插入
B)如果叶子节点满，父节点还没满，拆分叶子节点，将中间节点放入父节点中
  小于中间节点的放在父节点的左边，大于中间节点的放在父节点的右边
C)如果叶子节点满了，父节点也满了，拆分叶子节点，小于中间节点的放在左边
  大于中间节点的放在右边，拆分父节点小于中间节点的放在左边大于中间节点的
  放右边。中间节点放在上一层。以此类推。直到整颗树平衡。

B+TREE的删除操作

A)如果叶子节点高于填充因子，直接删除节点
B)如果叶子节点低于填充因子，且父节点高于填充因子，
  需要合并兄弟节
  更新父节点
C)如果叶子结点低于填充因子，且父节点低于填充因子，
  需要合并兄弟节点
  更新父节点
  合并父节点以及更新对应的节点